MOEA/D 简介

2019-06-14| Research||Word count: 4k|Reading time: 16 min

MOEA/D: A Multiobjective Evolutionary Algorithm Based on Decomposition

把一个多目标优化问题分解成一定数量的子问题，并同时优化他们。

各个子问题只会使用其相邻一系列子问题的信息。

I. Introduction

A. Basic Definition

MOP 定义: $maximize\ F(x)=(f_1(x),f_2(x),\cdots,f_m(x))^T\ subjuect\ to\ x\in\Omega$ (1)
$\Omega$ 定义: 决策空间 decision space， $F:\Omega\rightarrow R^m$
$R^m$ 定义: objective space
$\{F(x)|x\in\Omega\}$ : attainable objective set
限制：对于 $x\in R^n,\Omega=\{x\in R^n|h_j(x)\leq0,j=1,\cdots m\}$ , $h_j$ are continuous function，这使得 $x$ 的定义域被限制在一定范围，此时前面那个方程被成为一个连续多目标优化问题。
Domination: $\forall i\in \{1,\cdots,m\},u_i\geq v_i$ and $\exist j\in \{1,\cdots,m\},u_i> v_i$ ，即全部大于等于，并至少有一个 index 大于的时候，称其为 $u_i$ dominates $v_i$
对于一个点 $x$ 如果 $F(x)$ 在目标域内没有被 dominated，其 $x$ 被称为 Pareto optimal， $F(x)$ 被称为 Pareto optimal vector
Pareto set (PS): all $x$ which is Pareto optimal point
Pareto front (PF): all $F(x)$ which is Pareto optimal vector

大多数多目标优化问题有无数的 Pareto optimal vector，其组成连续的PF。所以除非有时间，获取一个完整的PF将极其困难。所以找到一个在PF上均匀分布的Pareto optimal vector，使其能够很好代表PF。

B. Current Algorithm Analysis

这一部分的段落我个人没大看懂，因为没有基础的概念和常识以及也没读过其他基础演化算法的文章，只能先试着做出一些理解。

It is well-known that a Pareto optimal solution to a MOP, under mild conditions, could be an optimal solution of a scalar optimization problem in which the objective is an aggregation of all the $f_i$ ’s. Therefore, approximation of the PF can be decomposed into a number of scalar objective optimization subproblems. This is a basic idea behind many traditional mathematical programming methods for approximating the PF. Several methods for constructing aggregation functions can be found in
the literature (e.g., [1]). The most popular ones among them include the weighted sum approach and Tchebycheff approach. Recently, the boundary intersection methods have also attracted a lot of attention [9]–[11].

如果在一个标量优化问题中 objective 是所有 $f_i$ 的值的集合体，那么在一般情况下 Pareto 可能就是它的最优解。那么 PF 的估计就可以分解成若干标量优化子问题。权重向量和及切比雪夫接近是比较常用的两种 aggregation function。

目前主流的 MOEAs 并没有 decomposition 参与，它们把 MOP 视为一个整体来解决，亦不会把任何一个单独的解与标量优化问题相关联。
一般有一个 objective function 来衡量所有解最后只能得到一个最优值。
Domination 不会在目标空间中定义一个完整的解的顺序，而且 MOEA 主要负责产生尽量离散的 Pareto optimal point 以代表整个 PF。所以，传统的 selection operator 不能直接在 non-decomposition MOEA 中使用。
However, domination cannot provide a full ranking among all the solutions. (Engin Ufuk Ergul & Ilyas Eminoglu (2014) DOPGA)

如果存在一个 fitness assignment scheme 把一个解赋予一个相关的 fitness value 以显示此解的实用性，那标量优化 EA 可以直接扩展去处理 MOPs，当时主流的 fitness assignment strategies 有 alternating objective-based 比如 VEGA，domination-based 比如 PAES、SPEA-II、NSGA-II。

TPLS 会考虑一组 scalar optimization 问题，在这些问题中，目标是在 MOP 考虑下的一个聚类，一个 scalar optimization 算法会基于聚类的系数以一个顺序应用到这些问题上，上一个问题的解会被获取过来以作为下一个问题的起点，尽管他的聚类目标与之前的那个只有微小的区别。
MOGLS 会同时优化所有聚类使用 weighted sum approach 或者 Tchebycheff approach，在每次迭代，它会优化一个随机生成的聚类目标

C. MOEA/D

会把一个 MOP 分解成 N 个标量优化子问题
演化一个人口基数的解集以同时解决这些子问题
在每一代，人口都是由每个子问题最优的解组合而成
子问题之间的邻居关系是基于他们聚类参数向量之间的距离决定的
两个邻居子问题的最优解应该是十分相似的
每个子问题在 MOEA/D 的优化过程中，只会使用其邻居的信息

D. MOEA/D features

MOEA/D 以一个很有效率的方式把 decomposition approaches 引入多目标演化计算。而分解法，通常是在编程数学社区被发展过后，可以很好的纳入 MOEA/D 框架中的演化算法以解决 MOP
MOEA/D 优化 N 个标量优化问题，而不是把 MOP 作为一个整体去解决，像 fitness assignment 或者 diversity maintenance 会在 MOEAS 上产生困难的这些情况，在 MOEA/D 框架下能更容易去控制
MOEA/D每一代的计算复杂度都低于 NSGA-II 和 MOGLS
目标正则化的技巧可以纳入算法之中，以解决一些不同规模(disparately scaled)的目标
每个解都关联了一个标量优化问题，所以可以很自然地使用标量优化方法。相对应的，非分解的 MOEAs 并不能很容易的用到 scalar optimization methods 的好处

II. Decomposition of Multiobjective Optimization

A. Weighted Sum Approach

本方法考虑一个不同目标的凸组合：指点的线性组合，要求所有系数非负且合为1。此处的「点」可以是仿射空间中的任何点，包括向量和标量。

DEF:

weight vector:

$\pmb\lambda=(\lambda_1,\cdots,\lambda_m)^T,\ \lambda_i\geq0,\ \sum_{i=1}^{m} \lambda_i=1$

标量优化问题 (2)

$maximize\ g^{ws}(x|\pmb\lambda)=\sum_{i=1}^{m} \lambda_if_i(x)$

这是一个 pareto 最优点，生成一个 weight vector 集合来计算这个 PF。但并不是所有的 pareto optimal vector ( $F(x)$ ) 都可以从这个这个方法得到，比如非凹的 PFs

B. Tchebycheff Approach

DEF:

标量优化问题 (3)

$minimize\ g^{te}(x|\pmb\lambda,z^*)=\max_{1\leq i\leq m} \{\lambda_i|f_i(x)-z_i^*\}$

reference point

$\begin{aligned} z^*&=(z_1^*,\cdots,z_m^*)^T \\ z_i^*&=max\{f_i(x)|x\in \Omega\} \end{aligned}$

简单释义：去 minimize 距离 ref point 值最大的 index

对于每一个 pareto 最优点 $x^*$ 都存在一个权重向量 $\pmb\lambda$ 使得 $x^*$ 是方程(3)的最优解，且每一个(3)的最优解都是方程(1)的最优解。

于是可以通过调整权重向量来获取不同的 pareto 最优解。

缺点在于，对于一个连续优化的 MOP，这个方法不够平滑。

但是在这里他仍能使用，因为本文的算法不需要求得这个 aggregation 函数的导数。

C. Boundary Intersection (BI) Approach

为连续 MOP 而设计的 BI approach 比如 Normal-Boundary Intersection Method [9] 和 Normalized
Normal Constraint Method [10]。一般情况下，PF 在 maximize 下是最右上方的边界(minimize 是左下方)。通常 BI 是要找到一组线与 PF 的交点，所以如果这组线很均匀的分布的话，这些个交点就可以很好的代表这个 PF。

DEF:

$\begin{aligned} minimize\ g^{bi}(x|\pmb\lambda,z^*)&=d\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (4)\\ subject\ to\ z^*-F(x)&=d\pmb\lambda \\ x &\in \Omega \end{aligned}$

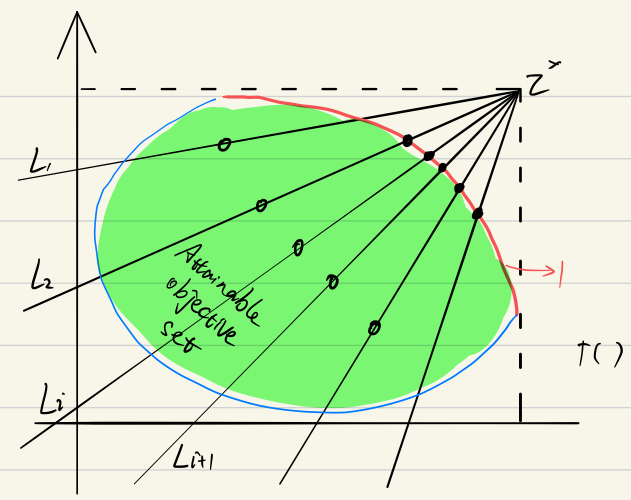
这是普通的 BI，weight vector 是从 ref point 发散出来的。目标就是把 $F(x)$ 一直向上推的越来越高，限制使得 $F(x)$ 始终在 $L$ 上。

所以这就有个缺点就是，需要不停的去把控那个等式的约束。由此本论文提出一个补偿(penalty)方法：

DEF:

$\begin{aligned} minimize\ g^{bip}(x|\pmb\lambda,z^*)&=d_1+\theta d_2\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (5)\\ subject\ to\ x &\in \Omega \end{aligned}$

where

$\begin{aligned} d_1&=\frac{||(z^*-F(x))^T\pmb\lambda||}{||\pmb\lambda||} \\ and\ d_2&=||F(x)-(z^*-d_1\pmb\lambda)|| \end{aligned}$

PBI

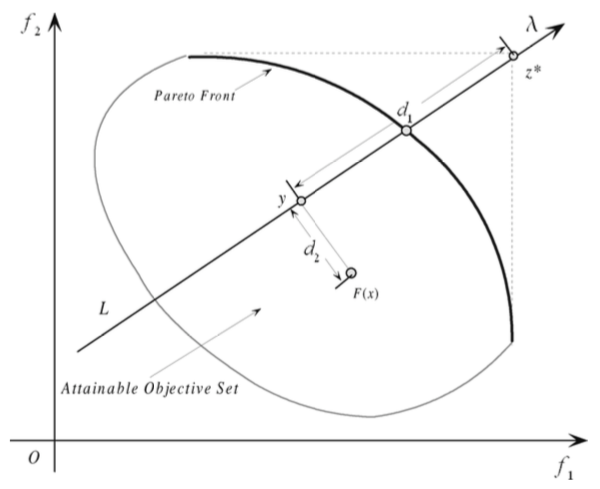
这里的要点就是要看补偿参数 $\theta$ 怎么设置了。如果设置的好，(4)和(5)的解应该是很相近的。

PBI 的好处都有啥（与 TE 相比）：

PBI 的解的分布比 TE 更加均匀，尤其是在 weight vector 不是特别多的时候
TE 在 x dominate y 的情况下，也会有 $g^{te}(x|\pmb\lambda,z^*)=g^{te}(y|\pmb\lambda,z^*)$ ，如下图

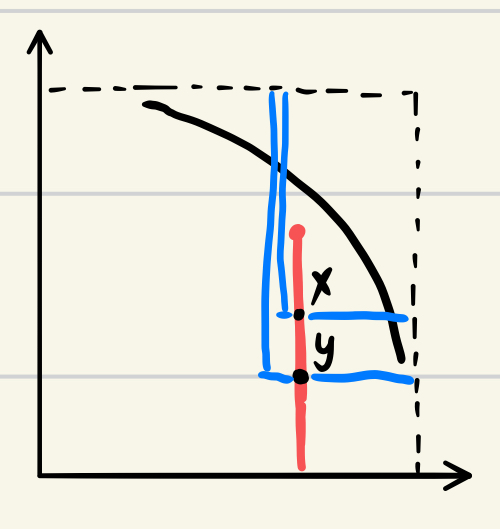
TE_bad

D. Summary

所以以上方法都可以用来把 PF 分解成一系列的单目标优化问题。当然也有很多种其他的 decomposition 办法，但是本文主要目标是研究算法框架的可行性以及效率，所以仅使用以上三种。

III. MOEA/D

A. General Framework

预设

假设如下描述中，我们都使用 TE 方法来分解，当然选哪种都可以，只需要做一些微小的变动即可。

$\pmb\lambda^1,…,\pmb\lambda^N$ 是均匀分布的权重向量

$z^*$ 是 ref point

所以第 $j$ 个 subproblem 即为

$minimize\ g^{te}(x|\pmb\lambda^j,z^*)=\max_{1\leq i\leq m} \{\lambda_i^j|f_i(x)-z_i^*\}$

这里注意到，我们首先有个预设就是理想的 PF 是一个连续的曲目，而且应该是比较平滑的(不平滑的正规化处理一下)，所以对于如果存在 $\pmb\lambda^i$ 和 $\pmb\lambda^i$ 他们如果离的很近的话，他们的解也应该是很相似的，所以他们离的比较近的就可以互相提供信息来进行优化

邻居：在 MOEA/D 里就是若干离当前权重向量很近的一系列权重向量，且他们仅会被当前权重向量利用以优化本 subproblems

在每一代 $t$ ，算法(with TE)会维护以下：

具有 $N$ 个解 $x^1, …, x^N$ 的总人口， $x^i$ 对应的是第 $i$ 个子问题的解
$FV^i,i=1,…,N$ 是对于第 $i$ 个解的 F value
$z=(z_1,…,z_m)^T$ ，这里面 $z_i$ 是对于目标 $f_i$ 目前所能达到的最优的值
还有一个 external population (EP) 来存放所有在搜索中发现的一些非统治地位的解，也就是最终结果

算法

a. INPUT

MOP
一个停止 criteria
$N$
$N$ 个均匀分布的权重向量 $\pmb\lambda^1,…,\pmb\lambda^N$
$T$ : 邻居的数量

b. OUTPUT

c. STEP

Step 1) Initialization
Step 1.1) $EP=\empty$
Step 1.2) 计算任意两个权重向量之间的欧式空间距离，算出 $T$ 个邻居 $B(i)=\{i_1,…,i_T\}$ ，然后 $\pmb\lambda^{i_1},…,\pmb\lambda^{i_T}$ 即为那些邻居
Step 1.3) 根据题设生成基础人口 $x^1, …, x^N$ ，设置 $FV^i=F(x_i)$
Step 1.4) 初始化 $z$

Step 2) Update
For i = 1,…,N Do
Step 2.1 繁殖) 从邻居 $B(i)$ 中随机选择两个 $k,l$ ， $x^k,x^l$ 由基因操作子来产生子代 $y$
Step 2.2 增强) 对 $y$ 使用一个题设的修复/增强的启发式方法，产生 $y'$
Step 2.3 更新 $\pmb z$ ) 用 $y'$ 来更新 $z$
Step 1.4 更新邻居) 对于邻居 $B(i)$ 中的每个 $j$ ，如果 $g^{te}(y'|\pmb\lambda^j,z) \leq g^{te}(x^j|\pmb\lambda^j,z)$ ，则 $x^j=y',FV^j=F(y')$
Step 1.4 更新 EP) 移除 EP 中所有被 $F(y')$ dominate 的解，然后把 $F(y')$ 加入

Step 3) Stopping 如果满足停止条件，输出 EP，否则重复 STEP2

d. 注

其向量本身也属于邻居中的一个，因为距离为0

B. Discussions

为什么只考虑有限数量个子问题

MOGLS 就是每代随机生成新的权重向量，要知道我们只需要有限个均匀分布的解来表示 PF 就可以了，所以这个方法既现实又合理，可节约计算资源
多样化

Section I 中说过 MOEA 需要维持一个多样化的人口来产生一系列具有代表性的解。NSGA-II and SPEA-II use crowding distances among the solutions in their selection to maintain diversity. 但那些算法并不是很容易就能产生一个均匀分布的目标向量。MOEA/D 中每个子问题和每个人口相关联，而且权重向量也是选取的很恰当，所以可以保证解的均匀分布性
Mating Restriction and the Role of T in MOEA/D

一个新解的产生仅基于邻居中的父母，所以如果邻居太小，子代会与父母具有极高的相似性，不利于人口多样性与探索解的新的区域，但如果邻居太大，父母又是不能很好的去优化本子问题，所以 exploration ability 也会变得很差。

C. Variants of MOEA/D

可以用不同的 decomposition method
返回结果的时候可以使用 final population，如果 EP 没有被维护的话。(以及再加上 EP size 的限制) [21]
cMOGA 也可以被视为使用了 decomposition 但并不能维持一个最佳解集 [40]

Other

至此论文只写到了三分之一的位置，后面大篇幅都是在讲与 MOGLS/NSGA-II 的对比以及在背包问题上的应用。

IV. COMPARISON WITH MOGLS
- A. 什么是 MOGLS
- B. MOEA/D 和 MOGLS 的时空复杂性的对比
  |||我觉得这部分我还得在暑假看一下计算理论的书才能知道详细步骤，而且毕竟也是要考的
- C. 什么是多目标 01背包问题(MOKP)
- D. MOEA/D 和 MOGLS 在 MOKP 上的实现方法，算法步骤
- E. 实验参数设置
- F. 然后就是一堆实验结果
V. MOEA/D 与 NSGA-II 在连续性 MOP 上的对比
说到连续性，就是那些 continuous function，通常只是一个简单的函数而已
- A. 会有 Test Suites: ZDT, DTLZ 等跑分函数
- B. 什么是 NSGA-II，(步骤是真的少，那篇文读了才开头)
- C. 使用 MOEA/D 的变体
- D. 两者复杂性分析
- E. 实验参数设置
- F. 实验结果
- G. MOEA/D 扩展
VI. 结论
居然姚新被 Acknowledge 了，zhou和lucas也被提及了，zqf是真的巨

所以这后三分之二我在写这提及的两个算法之后才会去仔细读一下，在这之前也会增加 NMOP [1] 的练习

REFERENCES

[1] K. Miettinen*, Nonlinear Multiobjective Optimization*. Norwell, MA: Kluwer, 1999.

[9] I. Das and J. E. Dennis, “Normal-bounday intersection: A new method for generating Pareto optimal points in multicriteria optimization prob- lems,” SIAM J. Optim., vol. 8, no. 3, pp. 631–657, Aug. 1998.

[10] A.Messac,A.Ismail-Yahaya,andC.Mattson,“Thenormalizednormal constraint method for generating the Pareto frontier,” Struct Multidisc. Optim., vol. 25, pp. 86–98, 2003.

[21] J. D. Knowles and D. Corne, “Properties of an adaptive archiving algo- rithm for storing nondominated vectors,” IEEE Trans. Evol. Comput., vol. 7, no. 2, pp. 100–116, Apr. 2003.

[40] T. Murata, H. Ishibuchi, and M. Gen*,* “Specification of Genetic Search Direction in Cellular Multiobjective Genetic Algorithm,” in Evolutionary Multicriterion Optimization. Berlin, Germany: Springer-Verlag, 2001, LNCS1993, pp. 82–95.